Is Picking Two Marbles Permutation

If we want to figure out how many combinations we have we just create all the permutations and divide by all the redundancies.

Is picking two marbles permutation. There s two green marbles in the bag. Endgroup jessica oct 6 13 at 3 36. It is crucial that you are choosing items without replacement for the two methods to be equivalent. Choosing a first marble then a second is the same as first choosing two marbles then picking which goes first.

Assuming each color of marble is identical and it doesn t matter which specific marble of each color is chosen calculate the number of possible permutations in which you can remove the 10 marbles. Or 6 variations for every choice we pick. 1 after marble no 2 is different from vice versa. If we randomly select two marbles from the bag what is the probability that the selected marbles are of different colors in other words one white and one red.

There s one blue marble. A draw the tree diagram for the experiment. Why do the two solutions differ. Endgroup sudarsan oct 6 13 at 3 24 begingroup assuming the marbles are identical and order doesn t matter.

For example given that we have 5 different colored marbles blue green red yellow and purple if we choose 2 marbles at a time once we pick the blue marble the next marble cannot be blue. You remove them from the bag one of the time without replacement. And sometimes this is referred to as the sample space the set of all the possible outcomes. Suppose an opaque jar contains 4 red marbles and 10 green marbles the following exercise refers to the experiment of picking two marbles from the jar without replacing the first o log on.

In our case we get 336 permutations from above and we divide by the 6 redundancies for each permutation and get 336 6 56. So i could pick that green marble or that green marble. And then there s one blue marble in the bag. Selecting k objects from n objects is given by.

Fancy word for just a simple idea that the sample. Algebra permutations solution. A jar contains 4 black marbles and 3 red marbles. There are 4 red marbles 3 yellow 2 green and 1 blue marble.

In this case you know whether both are red after the first step so the second step is not necessary and you can work with combinations. So if we have 3 tin cans to give away there are 3. For permutations without repetition we need to reduce the number of objects that we can choose from the set each time. B find probabilities for p bb p br p rb p ww p at least one red p exactly one red 3.

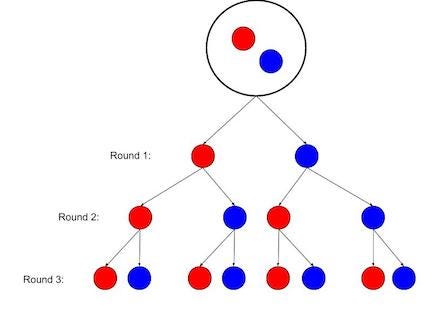
So this is all the possible outcomes.